Periódicamente, durante la pandemia de Covid-19, el personal científico de los CDC ha utilizado los datos de sus estudios disponibles para estimar la eficacia de las versiones actuales o recientes de las vacunas contra el Covid-19 para reducir el riesgo de dar positivo en una prueba de Covid-19. Si bien el hecho de “dar positivo” ha sido algo controvertido debido a los números de umbral secretos de PCR Ct involucrados que han permitido que personas no infecciosas con Covid-19 no reconocido de hace algunas semanas sigan dando positivo en la prueba, mi objetivo aquí es ilustrar Los problemáticos métodos epidemiológicos de los CDC que han inflado sustancialmente los porcentajes de eficacia de las vacunas que han informado.
Los estudios epidemiológicos controlados se dividen en tres y sólo tres diseños de estudio básicos. O se toma una muestra total de sujetos y se evalúa a cada sujeto tanto en cuanto a su estado de caso como a su estado de exposición previa (este es un estudio transversal) o se sigue una muestra de personas expuestas y una muestra de personas no expuestas para ver quién se convierte en un caso y quién se obtiene un control (un estudio de cohorte) o una muestra de casos y una muestra de controles, y cada sujeto se evalúa para determinar su estado de exposición pasada (este es un estudio de casos y controles). Si un estudio de cohorte implica asignar al azar a los sujetos entre expuestos y no expuestos, se trata de un ensayo controlado aleatorio (ECA), pero el diseño del estudio sigue siendo de cohorte.
En un estudio transversal y en un estudio de cohorte, la riesgos de obtener el resultado de interés (es decir, de ser un sujeto de caso, en este caso, dar positivo) se puede estimar para las personas expuestas por el número de casos entre los expuestos dividido por el número total de expuestos. Lo mismo ocurre con los no expuestos. Lo interesante es que la comparación de estos dos riesgos, el riesgo relativo (RR), es el riesgo de los expuestos dividido por el riesgo de los no expuestos. El RR estima cuánto peor es el riesgo entre los expuestos en comparación con los no expuestos. Para una vacuna u otra exposición que reduzca el riesgo, el RR será inferior a 1.0.
Los estudios transversales y de cohortes, por sus diseños muestrales, permiten estimar el RR a partir de sus datos. Sin embargo, los estudios de casos y controles no permiten estimar los riesgos de resultados, porque cambiar el número relativo de casos muestreados versus controles afecta cuáles serían las estimaciones de riesgo. En cambio, los estudios de casos y controles permiten estimar la odds del resultado, no del riesgo. Por ejemplo, probabilidades de 2:1 de que ocurra un evento. Este valor no se ve afectado por el diseño de muestreo. En los estudios de casos y controles, las probabilidades relativas (o odds ratio, OR) del resultado se estiman mediante las probabilidades del resultado entre los expuestos, divididas por las probabilidades entre los no expuestos.
Para una vacuna, su eficacia se estima en 1.0 – RR. Para los datos de estudios de casos y controles que solo estiman OR y no el RR, ¿cuándo el OR se aproxima al RR con suficiente precisión como para sustituirlo en esta fórmula? Esta pregunta tiene una historia epidemiológica detallada más allá del alcance actual, pero en el sentido más simple, el OR se aproxima al RR cuando en la población los casos son poco frecuentes en comparación con los controles.
Pasemos ahora a los CDC y sus errores epidemiológicos sistemáticos. En un análisis reciente, Link-Gelles y colegas tomaron una muestra de un total de 9,222 personas sintomáticas similares a Covid-19 elegibles que solicitaron pruebas de Covid-19 en las farmacias CVS y Walgreen Co. durante el 21 de septiembre de 2023 hasta el 14 de enero de 2024. Evaluaron el estado de vacunación anterior de cada individuo, así como la positividad. del resultado de la prueba. Por definición, este es un estudio transversal, porque no se tomaron muestras de números individuales de casos y controles, o de números individuales de expuestos (vacunados) y no expuestos (no vacunados). Sólo se muestreó el número total de sujetos.
Sin embargo, los investigadores estimaron el OR, no el RR, a partir de estos datos, mediante el uso de un método de análisis estadístico llamado regresión logística que permite ajustar el OR según varios posibles factores de confusión. No hay nada de malo en utilizar la regresión logística y obtener OR estimadas en cualquier diseño de estudio; el problema es utilizar el valor OR en lugar del RR en la fórmula de eficacia de la vacuna 1.0 – RR. Debido a que el diseño del estudio fue transversal, los investigadores podrían haber examinado la ocurrencia relativa de casos en la población a partir de los números de muestra, pero no parecieron hacerlo. De hecho, los casos comprendieron 3,295 del total de 9,222 muestreados, el 36%, lo que no es lo suficientemente pequeño como para utilizar el quirófano como sustituto del RR. Esto es cierto tanto entre los sujetos expuestos (25%) como entre los no expuestos (37%).
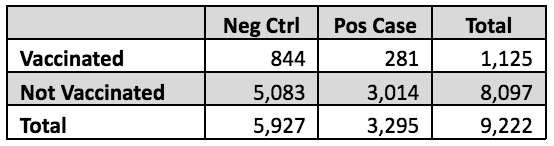
Sin embargo, es posible tener una idea aproximada de cuánto afectó esta mala suposición a la eficacia general de la vacuna del 54% afirmada por los autores. El número relevante de sujetos, que se muestra en la siguiente tabla, se indica en las Tablas 1 y 3 del artículo de Link-Gelles. El cálculo del RR a partir de estos datos sin procesar es simple. El riesgo en los vacunados es 281/1,125 = 25%; en los no vacunados, es 3,014/8,097 = 37%. El RR es la proporción de estos dos, 25 %/37 % = 0.67, por lo que la eficacia de la vacuna basada en estos datos brutos sería 1.0 – 0.67 = 0.33 o 33 %.
De manera similar, a partir de estos datos brutos se puede estimar el OR como 0.56, que si se usara en la fórmula de eficacia de la vacuna daría una eficacia del 44%, apreciablemente diferente del 33% de eficacia estimado correctamente utilizando el RR.
Sin embargo, Link-Gelles et al. utilizaron el OR ajustado = 0.46 obtenido de su análisis de regresión logística. Esto difiere del OR no ajustado = 0.56 por un factor de 0.46/0.56 = 0.82. Podemos utilizar este factor de ajuste, 0.82, para aproximar lo que habría sido el RR bruto si se hubiera ajustado por los mismos factores: 0.67*0.82 = 0.55. Estas cifras se muestran en la siguiente tabla y demuestran que la eficacia correcta de la vacuna es aproximadamente del 45 %, no del 54 % afirmado, y menos del nivel nominal deseado del 50 %.

Como epidemiólogo, no tengo claro por qué mis colegas de los CDC habrían utilizado por error el OR como sustituto del RR cuando el supuesto requerido para esta sustitución no se cumplía y era fácilmente comprobable con sus propios datos. Han cometido este error en otro lugar (Tenforde et al.), donde también marcó una diferencia considerable en la eficacia de la vacuna, aproximadamente el 57% frente al 82% afirmado. Quizás los autores pensaron que el único método disponible para ajustar múltiples variables de confusión era la regresión logística que utiliza el OR, pero la regresión de riesgo relativo para ajustar el RR ha estado disponible durante mucho tiempo en varios paquetes comerciales de análisis estadístico y se implementa fácilmente (enebro).
Me parece sorprendente que aparentemente ninguno de los más de 60 autores entre los artículos de Link-Gelles y Tenforde reconociera que el diseño muestral de sus estudios era transversal, no de casos y controles, y por tanto que el parámetro adecuado a utilizar para estimar la eficacia de la vacuna era el RR, no el OR, y que en sus datos no se cumplía el supuesto de enfermedad rara para sustituir el OR por el RR. Por lo tanto, estos estudios sobrestimaron sustancialmente las verdaderas eficacias de las vacunas en sus resultados. Esta no es una cuestión puramente académica, porque las decisiones de política de salud pública de los CDC pueden derivarse de resultados incorrectos como estos.
Publicado bajo un Licencia de Creative Commons Atribución Internacional
Para reimpresiones, vuelva a establecer el enlace canónico en el original Instituto Brownstone Artículo y Autor.









